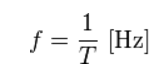どうも。りーず（leez）です。

ソニー等のメーカーやOTOTOYやe-onkyo musicなど、ハイレゾ対応のヘッドフォンを発売したり、ハイレゾ音源を配信したりするサービスが増えてきました。

iTunesを始め、AWAやLINE MUSIC、Amazon Prime Music、Spotify、mora、OTOTOYなど、ほぼ全てのデジタル配信・販売ストアへの登録サービスであるTuneCore Japanでは既に個人クリエイターがハイレゾ音源の販売をすることが可能です。

時代はハイレゾ時代に突入しつつあるということで、ハイレゾの高音質についてよくある誤解を解いていきます。

この記事の全体としてはハイレゾバンザイ！っていう内容です。

・マイクの限界はハイレゾに関係あるの？
・ハイレゾの本質は超高音ではない
・なぜ誤解が広まったのか

---

・マイクの限界はハイレゾに関係あるの？

多く見かけるのが、
「マイクはそもそも20kHzくらいが録音できる限界だから、ハイレゾなんて意味ないじゃん？」
「ハイレゾで高音域が聴こえるようになっても意味ないわ」
という主張です。
そして、これらは大きな間違いです。
（ただ、マイクに限界があるのは本当です。これは鋭いご指摘。）

結論からいうと、
「音の波がより細かく表現できるので、高音質になる。超高音はとりあえず置いておいて良い。
１秒間に記録できる点が増えるので、アナログ波形に近づく。」
というのが正解です。

どういうことか。
簡単に言うと、超高音が「表現できる」ということは、すべての音の波がより綺麗（なめらか）になるということです。

確かに20kHz以上の超高音を録音できるマイクってあんまり無いです。
一応あるようなのですが希少で、よほどのこだわりがないと買わないような高価なもののようです。

でも、問題はそこではないんです。
そもそも人間の聴力は20歳を過ぎると17kHzあたりを聴くのが精一杯で、徐々に衰えてもいきます。

・ハイレゾの本質は超高音ではない

よくデジカメで、「画素数」という単位が使われます。
500万画素より1000万画素のほうが綺麗なのはご存知の通り。
画素数は、「カメラのフィルターにある風景を、どれだけ細かく刻んで記録するか」ということです。
この細かい刻みの数値が、音の場合はHzだと思ってもらえればいいです。
（ハイレゾ表記など、音質を表すものの場合）

例えばCDは44100Hzの周波数までを再生できます。
これは1秒間に44100回の刻みで音の波形をデジタルデータにできる、ということです。（すごくざっくりとした説明です）

では、ハイレゾになるとどうなるか。
例えば192kHzのハイレゾになると、1秒間に192000回の刻みになります。
ですから、CDの4.35倍くらい「音を滑らかに刻め」ます。

ゲームや動画でいうと、「fps」と似ています。
30fpsと60fpsの動画だと、滑らかさが全然違いますよね。
（fps=フレームズ・パー・セカンド=frames per second。１秒間に何枚のフレーム（画像）を記録・表示出来るかの単位）

要は、周波数が高い音を記録できるというのは、音を凄く短いタイミングで刻む（記録・再生する）ことが可能になるということです。そうすると、元のアナログの線に近い滑らかな波形になって、高音質になるということです。

高音はものすごく小さい波です。
小さい波を表現できるということは、他の波のカーブもより滑らかになるということです。
ですので、低音・中域・高音、（そして超高音も）がより滑らかに表現できるようになります。

ここではざっくりとした解説なので、ハイレゾの定義やbitの話など、かなり割愛している部分があります。
（もし興味が出た人は調べてみてください。）

 

・なぜ誤解が広まったのか

ではなぜ高音ありきの議論になってしまうかというと、
「192kHzのハイレゾ」といわれると、多くの人は「高音（だけ）が再現できる」と考えてしまうのでしょう。

あとは、高校で物理選択をしている人が少ないので、
そもそも話がよく分からないというのもあると思います。

そんな訳で、ハイレゾになるということは素直に音が良くなるということで大丈夫です！

あとは、再生機でハイレゾに対応したものを選びましょう。

それについては

パソコンでハイレゾ音源を再生する環境を１万円程度で整える方法（Windows・Mac/ヘッドフォンで）

こっちでまとめています。

以上、ハイレゾについてのお話でした。

---

・おまけ（bitの話）

私は音楽制作を行っているのですが、例えばCD音質（44.1kHz/16bit）と48kHz/24bit（ハイレゾ音質）ではかなり音が違います。

ここまでHz（ヘルツ）の話をしておいてアレなのですが、本当は「bit（ビット）」の値のほうが音質に与える影響が大きいです。

この音質のbit（ビット）とは
「アナログの音の波の高低（タテ方向）をどのくらい細かくデータ化したか」
の数です。
タテ方向というのは、音の波の起伏のことです。波の高さのことです。

波は高くなったり低くなったりするので、それをどれだけ細かくデータ化できるか、という数値です。

・16bit = 2の16乗（16回掛ける） = 65,536段階 ≒ 約6万5千段階。

・24bit = 2の24乗（24回掛ける） = 16,777,216段階 ≒ 約1677万段階。

16bitと24bitではこれだけ違いがあるのが分かります。約6.5万 と 約1677万です。

（bitの話はかなり難しくなるので、ここは分からなくても全然大丈夫です。）

とりあえず、24bitは音が良いですよ。

---

以下、蛇足。

周波数fというのはヘルツ[Hz]という単位で表されます。

波の現象において、波長の周期を T [s] とすると、波の周波数 f [Hz] は次のように定義されます。
（[s]は秒のこと。）

周期Tというのは、１つの波の大きさ（秒数で換算した長さ）です。

「T」、つまり波の大きさが小さくなればなるほど周波数のfは大きくなります。
言い換えれば、周波数が大きいほど、小さい波（高音）だということです。

小さい波が表現できるということは、デジカメ同様、高画質ならぬ、高音質になるということです。